CMA均衡Matlab仿真实验
本文最后更新于 2024年8月6日 凌晨
CMA均衡算法实验
均衡是为了弥补信号在非理想信道下传播时对波形造成的失真进行“修补”,假如把信道输入到非理想信道再到信号输出的过程看作时域下信号与一个系统的系统函数卷积再加上特定的噪声的结果,那么均衡所做的就是拟合这个系统函数“求逆”的结果,使得经过信道的信号在经过这个“求逆”的操作后恢复原本的信号波形。大部分情况下,信道情况是未知的,在这种情况下对输出信道进行均衡的话有主要两种方法:依赖辅助数据进行信道估计和盲均衡方法。依赖辅助数据的方法就是在正式发送数据前先发送一段训练序列,通过已知的训练序列对比在接收端经过信道后的序列进行对比从而对信道进行估计,这种方法应用很广,在资源充足的情况下可以获得较好的效果,OFDM技术中长短训练序列的使用正是这一思想的体现:
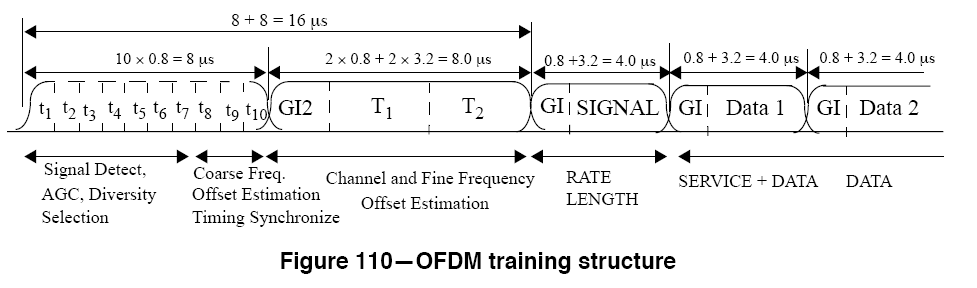
另一种方法则是不依赖训练序列的均衡方法,它靠接受到的信号进行自适应均衡,这种不依赖训练序列的方法称为盲均衡。下面的CMA(Constant Modulus Algorithm)即恒模算法就是隶属于Bussgang类盲均衡算法中的一种。CMA算法具有计算复杂度低,易于实时实现,收敛性能好等优点,代价函数只与接收序列的幅值有关,而与相位无关,故对载波相位不敏感。
CMA均衡原理
一般的均衡过程的原理框图如下所示:
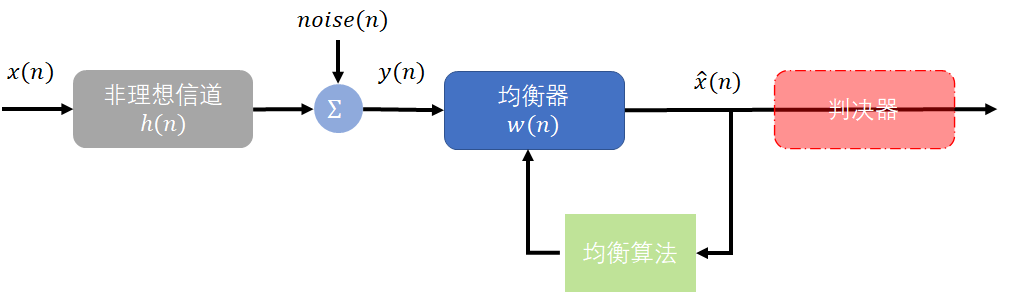
均衡器的输入信号可表示为:
其中,
均衡的目标即为通过改变滤波器参数组让输出的序列
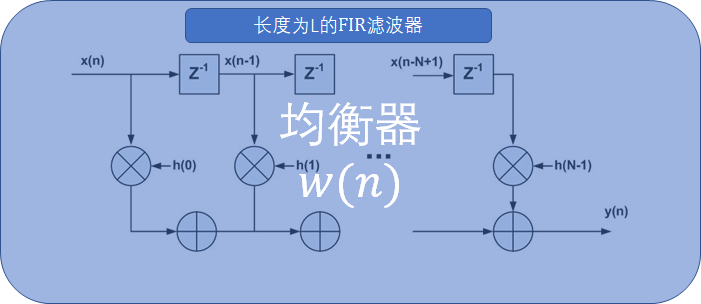
然而CMA算法不需要训练数据作为依赖, 它的本质是通过误差函数来迭代FIR滤波器的参数组
输入均衡其的符号序列表示为:
定义CMA算法的代价函数:
其中
其中,
求解上式可以使用梯度下降法,即对
将损失函数表达式代入上式,即可得到
CMA仿真实验
使用CMA算法均衡4QAM信号
采用4QAM对原始的3000个比特信息流进行调制,将调制后的信号经过参数矩阵为snr的高斯加性白噪声叠加作为均衡器输入的信号。对均衡器而言,设定三个不同的参数
原始的比特流经由4QAM调制后的星座图与经过信道与高斯加性白噪声(snr=10)叠加后的星座图:
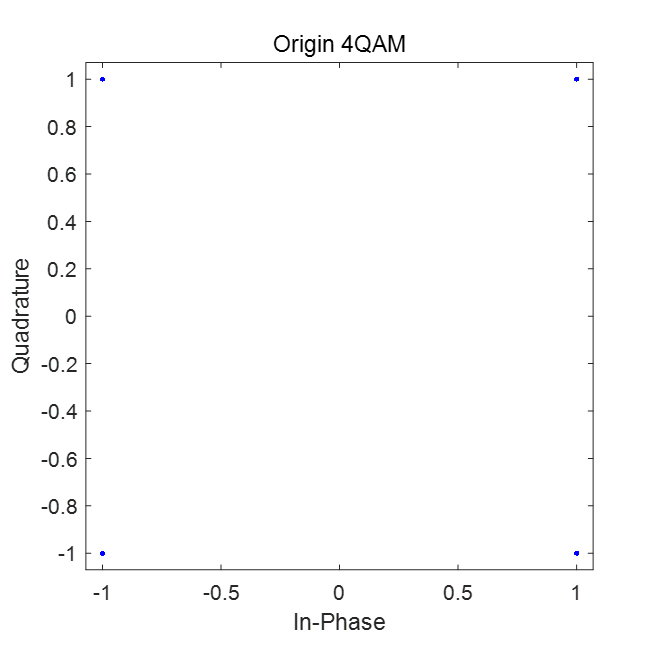
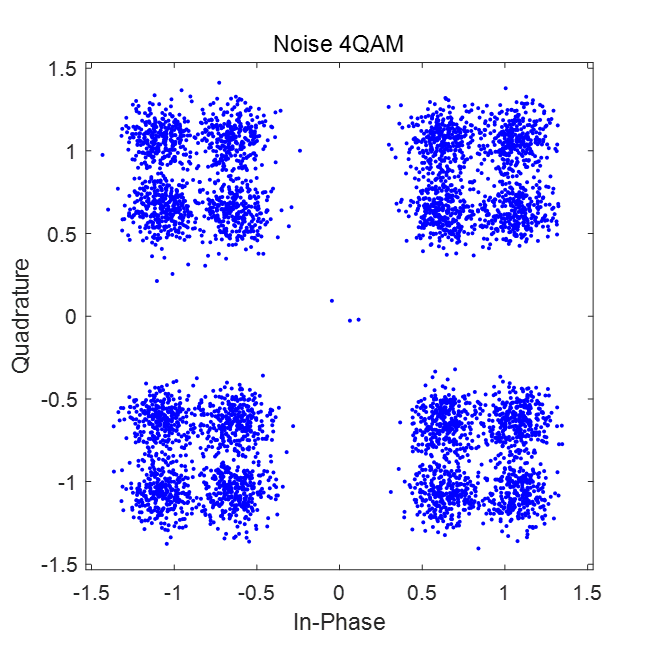
经过5000次迭代后,不同
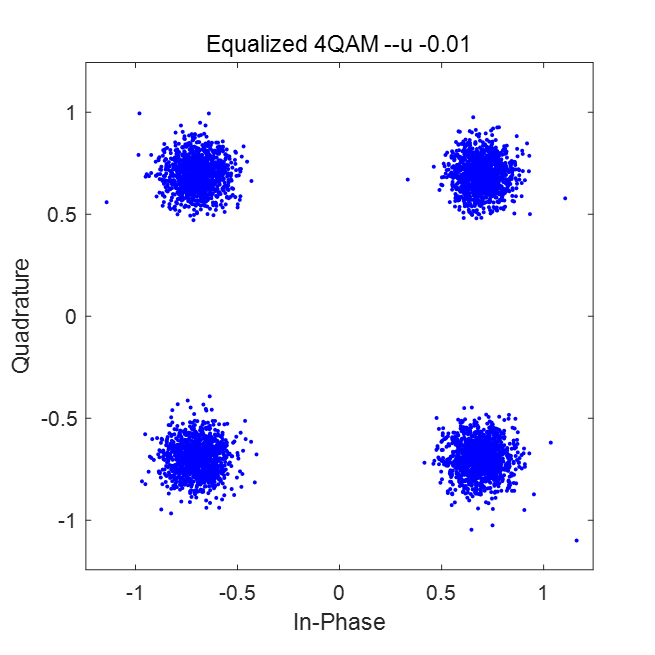
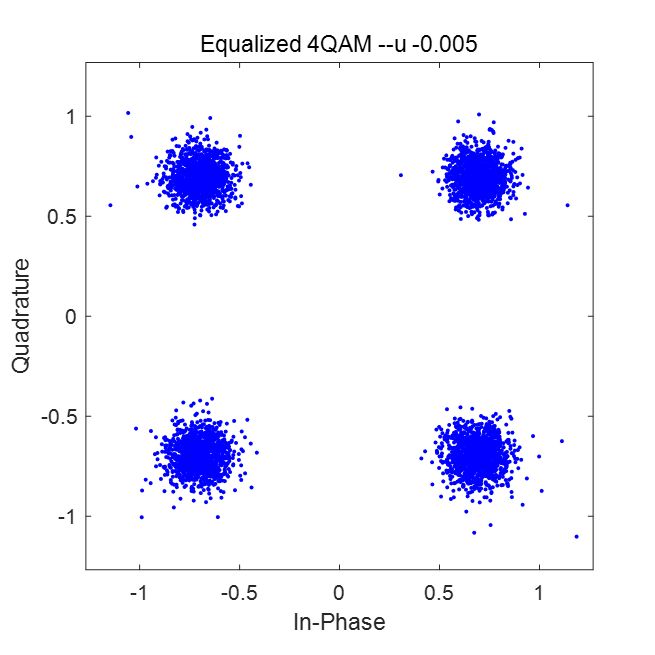
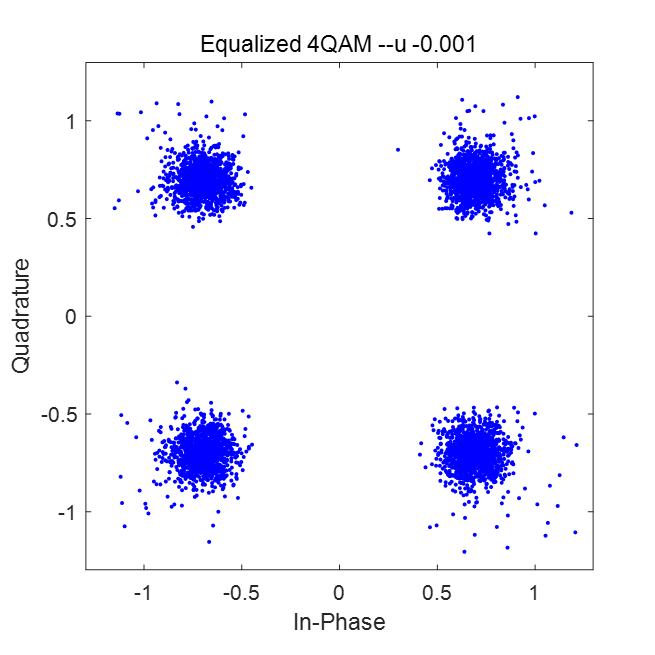
可以看到原本分散的符号聚拢在原始星座图的四个点附近。在信噪比较差(SNR=5dB)时,结果如图所示:

均衡后的星座图如下所示:
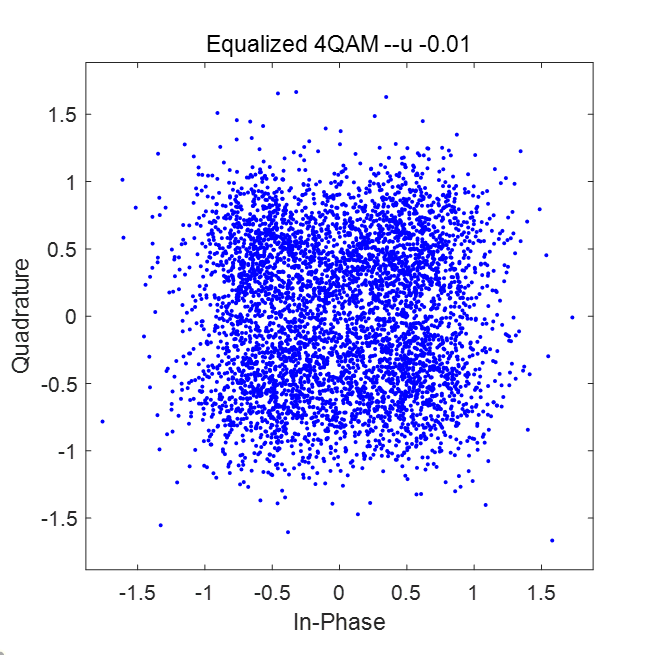
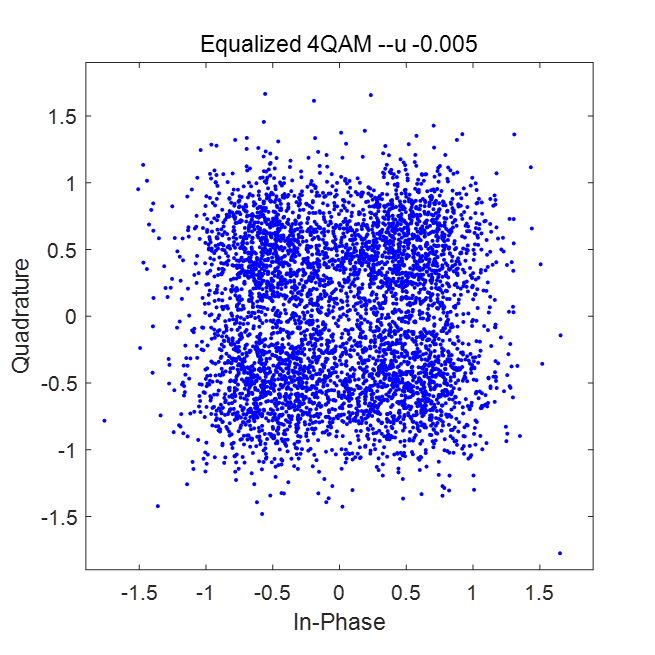
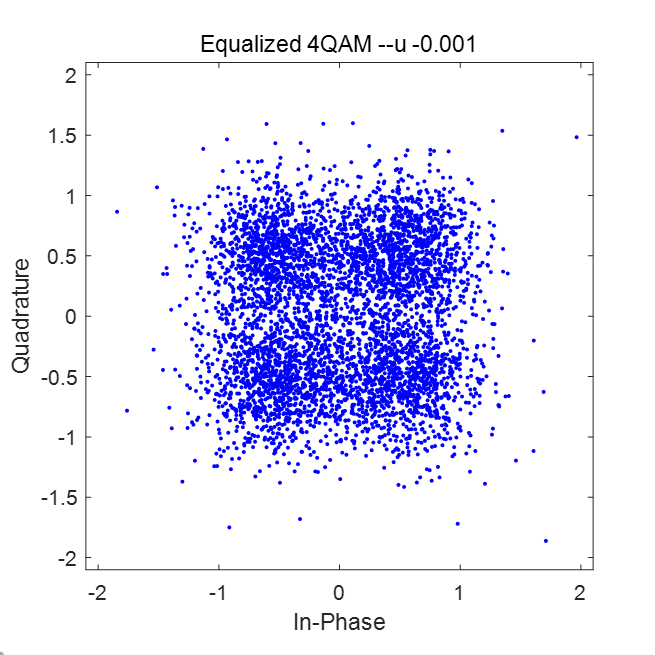
两种信噪比下,迭代次数与MSE关系对比如图:
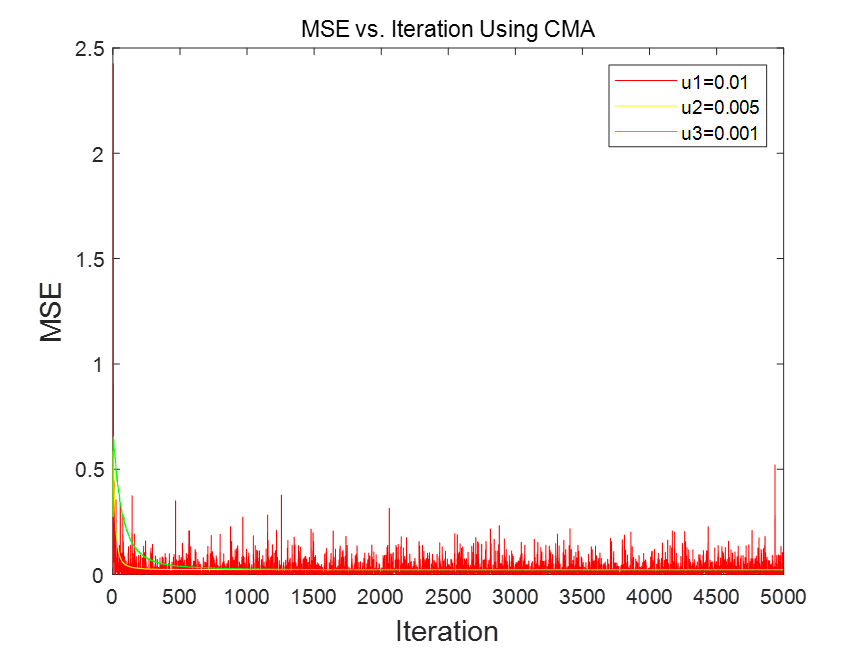
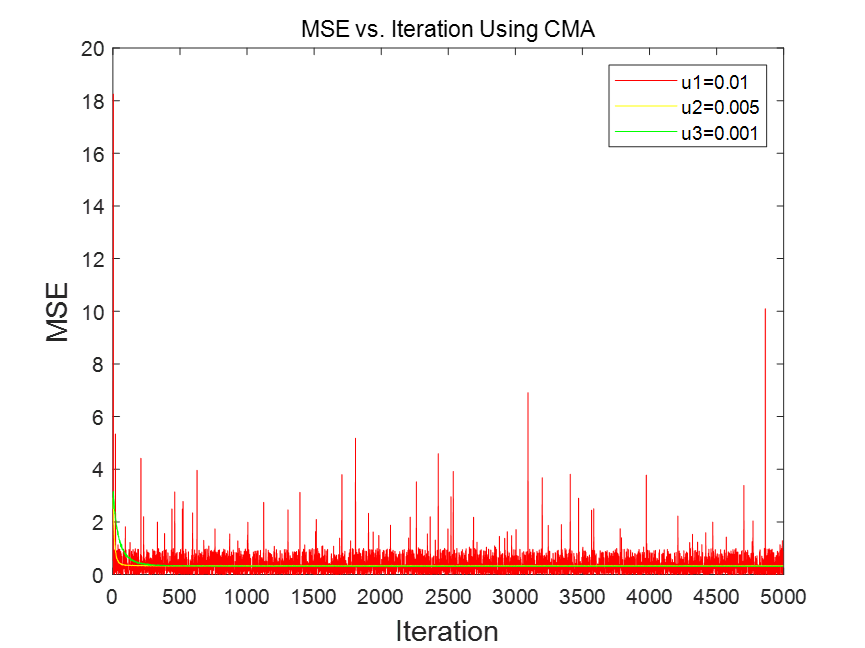
细节图:


可知
CMA算法对原始比特流波形影响
对于信号的原始比特流信息,经过调制后不好直观展示,因此使用OOK调制将比特映射到集合{-1,1}上,设定系统传输环境如下:
- 码元速率:10e9
- 码元抽样点数(过采样次数):8
- 码元个数:256
- 调制方式:OOK调制
- 判决门限:0.5
让信号序列经过高斯加性白噪声信道并经过均衡,在最终判决得到如下结果:

可以从图中看出均衡后的序列可还原出原本的信号波形,但会有一定的时滞。
附录
实验一代码
1 | |
实验二代码
1 | |